What is time complexity?

The term ‘time complexity’ is used to describe the efficiency of an algorithm with respect to its number of input elements. Defining the efficiency of an algorithm can be difficult while accounting for variables such as memory, disk, and network usage.
The Big O Notation is used to describe time complexity for the upper-bound runtime; the Big O is expressed for an algorithm's CPU usage alone, therefore discarding the other variables from consideration.

The Big O is part of a family of asymptotic notations which, include Big Theta Θ and Big Omega Ω.
The notations define the upper and lower asymptotic bounds for an algorithm. The Big O is only concerned with the approximate worst-case complexity of an algorithm; in other words, the guaranteed time in which an algorithm will complete.

Big O defines how the resources required (from the operations performed) in the algorithm scale up as the input elements to the algorithm grow.
The Big O does not reflect the performance of an algorithm. The performance of an algorithm would capture how much time or memory is consumed when the algorithm is executed.
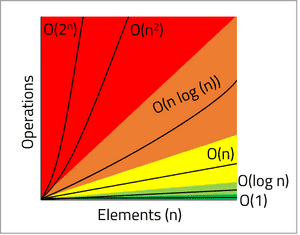
The graph below illustrates the 5 classifications an algorithm can have:

• Constant time O(1)

• Logarithmic time O(log n)

• Linear time O(n)

• N logarithmic time O(n log (n))

• Polynomial time O(n²) / Exponential time O(2ⁿ)

Defining the Big O of each operation

We are able to identify the Big O classification of each operation with the help of the Big O Cheat Sheet found here
Below are two examples of algorithms that capture a Big O classification themselves from a single operation:

Constant time O(1) translates to ‘Order of 1’. The resources required to complete the operation will not change as the input size grows. The below example illustrates an O(1) operation:

public void algorithm(List<Integer> values){
    System.out.println(values.get(0));
}

Linear time O(n), defines the linear growth of algorithm complexity in-line with the growth of elements. The below example illustrates an operation of O(n)

public void algorithm(int n){
    for (int i = 0; i<n; i++){
        System.out.println("got the value: " + i);
    }
}

The remaining classifications follow a pattern where the resources required will increase at the respective growth of n.
For example, typical sorting algorithms have a Big O notation of (n log (n)). The sorting algorithm would experience a resource requirement growth of (n log (n)) as the input elements increase by n.

Calculating the Big O of an algorithm

As algorithms will usually consist of multiple operations, we will use the example below to understand how we consider multiple operations into a Big O calculation:

public void calculateMaxValue(List<Integer> values){
    int max = 0;
    for(int i=0; i< values.size(); i++){
        if(values.get(i) > max){
            max = values.get(i);
        }
    }
    System.out.println("Max Value is: " + max);
}

Line 2 is used to initialise a variable. As this line is not influenced by the size of input values, line 2 has a Big O of O(1).
From lines 3 to 7, the function will loop through each member of values and identify if it is the maximum value of the List.
If values = {1,2,3,6,3}, the number of elements, n, will be 5.
The code block will run a total of 5 times in order to validate that the largest value is found within the list.
It will run for int i = 0,1,2,3, and 4 as values.size() = 5. A total of 5 operations for an input size of 5 means the code block has a Big O of O(n).
We can run through the code block again to support the Big O classification. If values = {1,2,3}, then values.size() will equal 3, and the number of operations ran will also be 3 (checking values of 1, 2, and 3).
Lastly, line 8 is used to print the result of the algorithm. This line is not influenced by the number of input values, therefore it is constant time and has a Big O of O(1).

As we account for the three operations within the algorithm, we have accumulated a Big O of: O(1) + O(n) + O(1).
The accumulation can be summarised into: 2 O(1) + O(n).
One defining characteristic of the Big O is that it is only defined by the rate of growth. Big O will not define how tightly an algorithm fits within the classification, but it will define the type of classification it falls within.

As we understand that it is only the type of growth we will consider, we can remove the constants from the accumulated Big O value.
As a result, 2 O(1) + O(n) is reduced to: O(1) + O(n).

The final reduction made to our Big O calculation involves releasing the non-dominant terms, in other words, an algorithm is only as efficient as its least efficient operation.
Working from the least-efficient classification of exponential growth, back to constant growth, we can identify the category the algorithm belongs as the classification that is satisfied first.

• Exponential/Polynomial time: ✘
• N logarithmic time: ✘
• Linear time: ✓
• Logarithmic time: ✘
• Constant time: ✓

We can see from the above checklist, the algorithm satisfies the linear time complexity first (from top-down).
It later satisfies constant time, however this is discounted as it is not the least efficient classification. As a result, the algorithm has a Big O Notation of constant time: O(n).

Conclusion

The Big O notation enables us to better understand how the individual operations within an algorithm can contribute to its upper-bound CPU consumption.
By breaking down an algorithm and understanding how the resource consumption of each operation will scale with the growth of input elements, we are better able to identify where possible inefficiencies lie.
Calculating the Big O will encourage you to explore and utilise the various data structures and methods available to create CPU-optimised algorithms.
The time complexity of our algorithms provide a measurable and reflective purpose for us to review how well each operation within our algorithms can scale with input elements.