Floating point primitives

The primitive data types float and double offer floating point values to be used for non-whole numbers. The JVM allocates floating point numbers a fixed size of memory: float consumes 4 bytes (32 bits), whereas double consumes 8 bytes (64 bits).
The benefits of using floating point numbers are their speed and efficiency. The JVM is able to very quickly calculate and store the values.

Binary fractions and floating point inaccuracies

The JVM stores floating points values as a binary representation of a fraction and exponent; floating point values are calculated using a Base 2 notation.
In calculus, the value of 0.1 can be calculated as 10^-1. Similarly, the value of 0.55 can be calculated as 55 * 10^-2.
The JVM calculates floating point numbers to the Base of 2. The Base 2 calculation is optimized within computers as their binary representation of 0's and 1's can be efficiently computed. The JVM is able to interpret the values without conversion and therefore enable floating point numbers to realise a benefit of efficiency with computational cost.

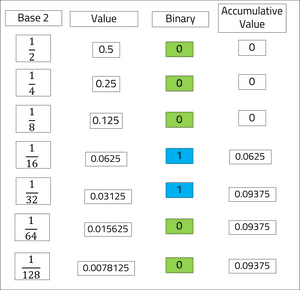
The example below demonstrates how the value of 0.01 can be defined in binary code.
The base of 2 is sequentially reduced by 1 from -1. The binary value indicates whether or not the value of Base 2 can increment the accumulative value towards 0.01.

The binary code of 0001100 will continue infinitely as 0's and 1's are added in pairs. The float and double primitive values will however round the value once their memory limit is reached. Some double values can be represented by a binary fraction within a finite length of the primitive data type and therefore does not require rounding. One example may be 0.75, it would be represented as 2^-1 + 2^-2 = 0.5 + 0.25 = 0.75.
As float and double primitives are not able to define the exact value of the decimal, they create unexpected results when applied to operations:

    double a = 0.2;
    double b = 0.19;

    float c = 0.2f;
    float d = 0.19f;

    System.out.println("double answer:  " + (a-b));
    System.out.println("float answer:   " + (c-d));

    double answer:  0.010000000000000009
    float answer:   0.010000005

Resolving floating point precision with math.BigDecimal

The Java math package introduces the BigDecimal class to enable control over the scale and precision of decimal numbers. The following example demonstrates how BigDecimal can resolve the precision inaccuracies of floating point values:

    BigDecimal e = new BigDecimal("0.2");
    BigDecimal f = new BigDecimal("0.19");  
    System.out.println("Big decimal answer: " + e.subtract(f));

    Big decimal answer: 0.01

How BigDecimal works

With the example of 1.23, scale refers to the number of decimal places with a base of 10 (2), and precision refers to the length of arbitrary numbers (3). BigDecimal uses the unscaled value (123) and the scale (10^-2) to create the precision value 1.23
As BigDecimal employs Base 10 calculations for the decimals, it can precisely represent all 2 decimal placed numbers. BigDecimal is typically used within applications that compute with currencies to ensure they are correctly represented.

The BigDecimal constructor can take arguments such as BigInteger, String, int, double, float, and char to convert into a BigDecimal. When supplying a BigInteger, the constructor can also take a scale argument to build the decimal:

    int a1 = 1;
    char a2 = 'a';
    double a3 = 2.4;
    String a4 = "2.4";
    BigInteger a5 = new BigInteger("1234");

    System.out.println("BigDecimal (int): " + new BigDecimal(a1));
    System.out.println("BigDecimal (char): " + new BigDecimal(a2));
    System.out.println("BigDecimal (double): " + new BigDecimal(a3));
    System.out.println("BigDecimal (String): " + new BigDecimal(a4));

    System.out.println("BigDecimal (BigInteger): " + new BigDecimal(a5));
    System.out.println("BigDecimal (BigInteger, scale): " + new BigDecimal(a5, 2));

BigDecimal (int):               1
BigDecimal (char):              97
BigDecimal (double):            2.399999999999999911182158029987476766109466552734375
BigDecimal (String):            2.4
BigDecimal (BigInteger):        1234
BigDecimal (BigInteger, scale): 12.34

The example above illustrates several ways a BigDecimal can be instantiated.
The use of double a3 on line 9 prints the binary value of 2.4 as a 32-bit integer. The String constructor on line 10 however prints the expected value of 2.4. Line 12 and 13 demonstrate how BigInteger can be used with a scale operation to build a decimal number.

The example above demonstrates the successful use of the String constructor with BigDecimal. The String constructor represents good practice as the BigDecimal no longer uses the binary fractions to create the value, and instead employs Base 10.

The BigDecimal class does not override operators such as + or - used for applying primitive data types to each other. Instead, methods such as add(), subtract(), multiply(), and divide() are implemented for operating with other BigDecimal instances.

BigDecimal Performance

The BigDecimal class introduces precision of decimal values by implementing Base 10 calculations. The final value, derived from the unscaled 32-bit value multiplied by 10^-scale results in a heavy performance cost to the application.
As a result, performance costs from BigDecimal can rise up to 90 times slower than using double. The decision to implement BigDecimal should strongly consider the importance of exact values to the context over speed.

Conclusion

The JVM uses binary functions to compute floating-point primitive values float and double. Their design enables the values to be efficiently calculated and stored.
The Base 2 function for deriving floating point values introduces a degree of precision loss from rounding. BigDecimal is a class within the math package of Java and enables decimal values to be computed against a Base 10. As a result, the decimal value created does not contain an unexpected rounded value.
BigDecimal is a useful class implemented with applications that handle currencies. BigDecimal however introduces performance costs that are to be considered with their use.